Mondegreen Generator

letters made out of salad ingredients — Word Salad

Rationale

Back in early 2019, when the “gibberish challenge” was bubbling up through the nascent “TikTok” milieu, I was compelled to discover an algorithm which, given arbitrary English input, could produce a “gibberish” phrase appropriate for the challenge.

I searched the web for such an algorithm, since surely someone had to have done this previously, but I didn’t find any results on GitHub, nor any discussions elsewhere.

There is a popular card game which operates on the same principle, cards have “gibberish” phrases and players must speak the phrases out loud to figure out the true meaning of what they are saying. This game has hundreds of cards, so I figured there was no way someone sat down and manually translated those into gibberish, but I could not find an answer to this online either. If the company which makes this card game does have such an algorithm, they are apparently not sharing it on the web.

I hate starting side-projects that already have satisfactory solutions available for free, since they seem to be a waste of my time, but this project presented enough of an interesting challenge to really pursue for at least a weekend.

So, I wrote the program, but haven’t really done anything with it since then (besides post the code to GitHub). I haven’t actively shared it in any way.

At first I wanted to create a website which would run the algorithm for the “TikTok” crowd to share, but by the time I was done with the implementation they had already moved past the fad. You have to be quick to catch the social media tidal waves I suppose. So, I left the project alone, content with the unfinished project and the single GitHub star from my college buddy.

⭐

But now it’s December 2021 – I’m reflecting on my year of coding and I’m ashamed to say that, besides adding ~2000 lines to my Emacs configuration and a single blog post I haven’t actually finished any side projects!

I think it’s time I change that.

I originally wrote the program in Clojure, partly to learn the idioms of the language, and partly to try out REPL-driven development, which Clojurians always claim is a “super power”. I don’t think I used enough tooling to consider myself a repl-superman, but I did find the experience to be satisfying, conducive to flow, and very fun.

For the uninitiated (or even the moderately initiated, like I was when I started), reading Clojure can be tricky, and as I documented my code with comments, I quickly realized the comments amounted to more lines than the code itself!

That’s when I learned about literate programming. Well, I had read some Knuth, so I was actually familiar with the concept of literate programming (did you know TeX was originally written as a single file?), but I didn’t actually realize it was easy with Clojure until I watched this video explaining the process plainly. It looked like something I could do (especially since I had been using org-mode for notes for over 2 years by that point), so I did it.

What am I doing?

The first step in any problem-solving endeavor is to outline exactly what the problem is, and the scope of the solution.

So what is the problem? Well, I want a function that can take English text and produce English text which sounds like the first, but is composed of different words.

After some Googling, I discovered that this type of language trick is known as a Mondegreen (or maybe more appropriately an Oronym, but I decided to go with Mondegreen).

So, what I want to create is a Mondegreen generator, a function which produces a Mondegreen given a list of words.

Overview of the problem-solving process

Because I didn’t know exactly how to solve this problem when I began, I needed to enable myself to explore the problem space.

This is where choice of technology becomes relevant. I needed a highly interactive environment, in order to develop solutions (and failures) as I went along.

I chose Clojure as my implementation language, partly because I just wanted to use it (after binging Rich Hickey’s talks on YouTube), and partly because the REPL-driven development paradigm fit my problem nicely.

So, I fired up a repl with clj, and got to work.

Data

Well, I got my repl started, and realized I had no data to work with. Data being the core of any program, I needed to make sure my sources would be sufficient.

Dictionary

The first thing I knew I would need was an English dictionary. Because my program would have to consume English text, it needed a way to distinguish English words from non-English words.

Phonemes

Unfortunately for the English language, the way a word is spelled has little to do with how it sounds, and for Mondegreens, the most important thing about the words is how they sound!

Luckily for me, I took an introduction to Linguistics course at my university, so I knew about phonemes:

In phonology and linguistics, a phoneme ˈfoʊniːm is a unit of sound that can distinguish one word from another in a particular language.

Phonemes are like the atoms of phonetics, the indivisible sounds a speaker makes to construct and distinguish words.

For example, even though “read” and “read” are spelled the same, the constituent phonemes help listeners discriminate between them:

read -> rēd
read -> rĕd

The first is the “long-e” sound, like in the word “reed”, while the other is the “short-e” sound, like in the word “red”.

For my program, I would also need a way to map a word to the list of phonemes that compose it. I searched Google (again) and came across the amazing Carnegie Melon Phonetic Dictionary, which is free to use and download here.

The Carnegie Melon Phonetic Dictionary

The dictionary actually solves both of my data needs! First, it is a dictionary, a function with the signature:

word -> boolean

verifying if a word is valid English, and also a phonetic dictionary, a function with the signature:

word -> [phoneme]

giving the list of phonemes that compose a valid English word. Lets explore the dictionary a bit.

Phones

This file (cmudict-0.7b.phones) describes the phonemes in the English language, it isn’t very large, which is kind of amazing given the huge diversity of words their composition can produce:

AA	vowel
AE	vowel
AH	vowel
AO	vowel
AW	vowel
AY	vowel
B	stop
CH	affricate
D	stop
DH	fricative
EH	vowel
ER	vowel
EY	vowel
F	fricative
G	stop
HH	aspirate
IH	vowel
IY	vowel
JH	affricate
K	stop
L	liquid
M	nasal
N	nasal
NG	nasal
OW	vowel
OY	vowel
P	stop
R	liquid
S	fricative
SH	fricative
T	stop
TH	fricative
UH	vowel
UW	vowel
V	fricative
W	semivowel
Y	semivowel
Z	fricative
ZH	fricative

The first column is the symbol the dictionary uses to represent that phoneme. Using the examples from earlier, we could translate to phonemes like so:

read -> "R IY D"
read -> "R EH D"

Exploring through code

Let’s parse this file to get a list of all the valid phonemes in our repl session.

(slurp "resources/cmudict-0.7b.phones")

"AA\tvowel\nAE\tvowel\nAH\tvowel\nAO\tvowel\nAW\tvowel\nAY\tvowel\nB\tstop\nCH\taffricate\nD\tstop\nDH\tfricative\nEH\tvowel\nER\tvowel\nEY\tvowel\nF\tfricative\nG\tstop\nHH\taspirate\nIH\tvowel\nIY\tvowel\nJH\taffricate\nK\tstop\nL\tliquid\nM\tnasal\nN\tnasal\nNG\tnasal\nOW\tvowel\nOY\tvowel\nP\tstop\nR\tliquid\nS\tfricative\nSH\tfricative\nT\tstop\nTH\tfricative\nUH\tvowel\nUW\tvowel\nV\tfricative\nW\tsemivowel\nY\tsemivowel\nZ\tfricative\nZH\tfricative\n"

Of course we will want to split the string by newlines:

(clojure.string/split-lines (slurp "resources/cmudict-0.7b.phones"))

["AA\tvowel" "AE\tvowel" "AH\tvowel" "AO\tvowel" "AW\tvowel" "AY\tvowel" "B\tstop" "CH\taffricate" "D\tstop" "DH\tfricative" "EH\tvowel" "ER\tvowel" "EY\tvowel" "F\tfricative" "G\tstop" "HH\taspirate" "IH\tvowel" "IY\tvowel" "JH\taffricate" "K\tstop" "L\tliquid" "M\tnasal" "N\tnasal" "NG\tnasal" "OW\tvowel" "OY\tvowel" "P\tstop" "R\tliquid" "S\tfricative" "SH\tfricative" "T\tstop" "TH\tfricative" "UH\tvowel" "UW\tvowel" "V\tfricative" "W\tsemivowel" "Y\tsemivowel" "Z\tfricative" "ZH\tfricative"]

And we also want to split on tabs (since this is a tab-separated file):

 (mapcat #(clojure.string/split % #"\t") (clojure.string/split-lines (slurp "resources/cmudict-0.7b.phones")))

("AA" "vowel" "AE" "vowel" "AH" "vowel" "AO" "vowel" "AW" "vowel" "AY" "vowel" "B" "stop" "CH" "affricate" "D" "stop" "DH" "fricative" "EH" "vowel" "ER" "vowel" "EY" "vowel" "F" "fricative" "G" "stop" "HH" "aspirate" "IH" "vowel" "IY" "vowel" "JH" "affricate" "K" "stop" "L" "liquid" "M" "nasal" "N" "nasal" "NG" "nasal" "OW" "vowel" "OY" "vowel" "P" "stop" "R" "liquid" "S" "fricative" "SH" "fricative" "T" "stop" "TH" "fricative" "UH" "vowel" "UW" "vowel" "V" "fricative" "W" "semivowel" "Y" "semivowel" "Z" "fricative" "ZH" "fricative")

You know what, let’s ignore the second column entirely, i.e. every 2nd entry (since we are only after the phonemes themselves):

(take-nth 2 (mapcat #(clojure.string/split % #"\t") (clojure.string/split-lines (slurp "resources/cmudict-0.7b.phones"))))

("AA" "AE" "AH" "AO" "AW" "AY" "B" "CH" "D" "DH" "EH" "ER" "EY" "F" "G" "HH" "IH" "IY" "JH" "K" "L" "M" "N" "NG" "OW" "OY" "P" "R" "S" "SH" "T" "TH" "UH" "UW" "V" "W" "Y" "Z" "ZH")

Finally, I think we will want a Set of phonemes, instead of a list, since there is really no order to these entries.

(set (take-nth 2 (mapcat #(clojure.string/split % #"\t") (clojure.string/split-lines (slurp "resources/cmudict-0.7b.phones")))))

#{"T" "CH" "K" "HH" "UH" "AY" "AH" "OW" "L" "JH" "UW" "G" "EH" "M" "OY" "S" "Y" "EY" "Z" "R" "F" "AW" "IY" "B" "SH" "P" "V" "TH" "IH" "AA" "AO" "N" "DH" "W" "ZH" "NG" "D" "ER" "AE"}

That looks pretty good, let’s save it into a variable:

(def phonemes (set (take-nth 2 (mapcat #(clojure.string/split % #"\t") (clojure.string/split-lines (slurp "resources/cmudict-0.7b.phones"))))))

#'user/phonemes

Fixing the “nested s-expressions” problem

One ugly thing about the solution we just composed is that every time we want to apply a new function to the previous result, we have to nest that previous result inside the new function call. This leads to deeply nested expressions which can be difficult to read.

Clojure’s answer to this problem is called the “threading macro” ->>

The below expression is equivalent to what we created above:
```
(def phonemes
  (->>
   (slurp "resources/cmudict-0.7b.phones")
   (clojure.string/split-lines)
   (mapcat #(clojure.string/split % #"\t"))
   (take-nth 2)
   (set)))
```
```
#'user/phonemes
```

Dict

This is the mapping of English words to their phonemes, using the phones described above.

It begins with a few lines of licensing comments (denoted by ‘;;;’).

;;; # CMUdict  --  Major Version: 0.07
;;;
;;; # $HeadURL: http://svn.code.sf.net/p/cmusphinx/code/trunk/cmudict/cmudict-0.7b $
;;; # $Date:: 2015-02-18 20:42:08 -0500 (Wed, 18 Feb 2015)      $:
;;; # $Id:: cmudict-0.7b 12857 2015-02-19 01:42:08Z air         $:
;;; # $Rev:: 12857                                              $:
;;; # $Author:: air                                             $:
;;;
;;; #
;;; # ========================================================================
;;; # Copyright (C) 1993-2015 Carnegie Mellon University. All rights reserved.
;;; #
;;; # Redistribution and use in source and binary forms, with or without
;;; # modification, are permitted provided that the following conditions
;;; # are met:
;;; #
;;; # 1. Redistributions of source code must retain the above copyright
;;; #    notice, this list of conditions and the following disclaimer.
;;; #    The contents of this file are deemed to be source code.
;;; #
;;; # 2. Redistributions in binary form must reproduce the above copyright
;;; #    notice, this list of conditions and the following disclaimer in
;;; #    the documentation and/or other materials provided with the
;;; #    distribution.
;;; #
;;; # This work was supported in part by funding from the Defense Advanced
;;; # Research Projects Agency, the Office of Naval Research and the National
;;; # Science Foundation of the United States of America, and by member
;;; # companies of the Carnegie Mellon Sphinx Speech Consortium. We acknowledge
;;; # the contributions of many volunteers to the expansion and improvement of
;;; # this dictionary.
;;; #
;;; # THIS SOFTWARE IS PROVIDED BY CARNEGIE MELLON UNIVERSITY ``AS IS'' AND
;;; # ANY EXPRESSED OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO,
;;; # THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR
;;; # PURPOSE ARE DISCLAIMED.  IN NO EVENT SHALL CARNEGIE MELLON UNIVERSITY
;;; # NOR ITS EMPLOYEES BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL,
;;; # SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT
;;; # LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE,
;;; # DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY
;;; # THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT
;;; # (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE
;;; # OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
;;; #
;;; # ========================================================================
;;; #
;;;
;;;  NOTES  ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;
;;;  [20080401] (air)  New dict file format introduced
;;;   - comments (like this section) are allowed
;;;   - file name is major version; vers/rev information is now in the header
;;;
;;;
;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;

And then continues to the dictionary itself, cmudict-0.7b.

The first few-dozen lines are actually the phonetic pronunciations of symbols like “!”, “#”, etc. so they are a bit strange, but we can still see the structure the dictionary:

!EXCLAMATION-POINT  EH2 K S K L AH0 M EY1 SH AH0 N P OY2 N T
"CLOSE-QUOTE  K L OW1 Z K W OW1 T
"DOUBLE-QUOTE  D AH1 B AH0 L K W OW1 T
"END-OF-QUOTE  EH1 N D AH0 V K W OW1 T
"END-QUOTE  EH1 N D K W OW1 T

You might be asking “Why do some of the phonemes have numbers?”, this is meant to indicate which phonemes are stressed, something I want to completely disregard (the whole point of a mondegreen is to stress different phonemes from the statement being deciphered).

So, when we parse the dictionary, let’s make sure not to include those characters:

(def dictionary-chars #"^[A-Z'\-\.\_]+")

(defn normalize-string
  "Converts a symbol found in the dictionary to just it's phonetic part
  (i.e. no stress)"
  [sym]
  (re-find dictionary-chars sym))

#‘user/dictionary-chars
#‘user/normalize-string

(normalize-string "AH0")

"AH"

Let’s test some examples in the repl to make sure the substitutions produce valid phonemes. First, we need to get a list of all the lines in the dictionary:

(def dictionary-lines
  (->>
  (slurp "resources/cmudict-0.7b")
   (clojure.string/split-lines)
   (filter (complement #(.startsWith % ";")))))

#'user/dictionary-lines

(take 10 dictionary-lines)

("!EXCLAMATION-POINT  EH2 K S K L AH0 M EY1 SH AH0 N P OY2 N T" "\"CLOSE-QUOTE  K L OW1 Z K W OW1 T" "\"DOUBLE-QUOTE  D AH1 B AH0 L K W OW1 T" "\"END-OF-QUOTE  EH1 N D AH0 V K W OW1 T" "\"END-QUOTE  EH1 N D K W OW1 T" "\"IN-QUOTES  IH1 N K W OW1 T S" "\"QUOTE  K W OW1 T" "\"UNQUOTE  AH1 N K W OW1 T" "#HASH-MARK  HH AE1 M AA2 R K" "#POUND-SIGN  P AW1 N D S AY2 N")

Now, what happens when a word has multiple possible pronunciations? Let’s look at the entry for “THE”:

THE  DH AH0
THE(1)  DH AH1
THE(2)  DH IY0

We need to remove the (1) and (2) so that these spellings will be the same. Luckily, we can normalize the spellings in the same way we normalized the phonemes, by disallowing numerics and parentheses.

Then, we ought to split the dictionary lines into (spelling phonemes) pairs, being sure to transform the spellings and phonemes into the normalized form we want (no numbered spellings, and no stress indicators on phonemes):

(def spellings+phonemes
  (map (fn [line]
         (->>
          (clojure.string/split line #"\s") ; split lines by space
          (filter #(not-empty %))           ; remove empty strings (from whitespace separation)
          (map normalize-string)            ; normalize
          (split-at 1)                      ; split into spelling + phonemes
          ((fn [[[spelling] phonemes]] [spelling phonemes])))) ; destructure the spelling list
       dictionary-lines))

#'user/spellings+phonemes

(rand-nth spellings+phonemes)

["SOUTHERN'S" ("S" "AH" "DH" "ER" "N" "Z")]

Much better. I should check that all the “spellings” and “phonemes” are each non-empty, in case there were some other data anomalies I didn’t find at the beginning of the file.

(filter (fn [[spelling phonemes]] (or (empty? spelling) (empty? phonemes))) spellings+phonemes)

(EH K S K L AH M EY SH AH N P OY N T)
(K L OW Z K W OW T)
(D AH B AH L K W OW T)
(EH N D AH V K W OW T)
(EH N D K W OW T)
(IH N K W OW T S)
(K W OW T)
(AH N K W OW T)
(HH AE M AA R K)
(P AW N D S AY N)
(SH AA R P S AY N)
(P ER S EH N T)
(AE M P ER S AE N D)
(B IH G IH N P ER EH N Z)
(IH N P ER EH N TH AH S IY Z)
(L EH F T P ER EH N)
(OW P AH N P ER EH N TH AH S IY Z)
(P ER EH N)
(P ER EH N Z)
(P ER EH N TH AH S IY Z)
(K L OW Z P ER EH N)
(K L OW Z P ER EH N TH AH S IY Z)
(EH N D P ER EH N)
(EH N D P ER EH N Z)
(EH N D P ER EH N TH AH S IY Z)
(EH N D DH AH P ER EH N)
(P ER EH N)
(P ER EH N Z)
(R AY T P EH R AH N)
(AH N P ER EH N TH AH S IY Z)
(P L UH S)
(K AA M AH)
(S L AE SH)
(TH R IY D IY)
(TH R IY D IY)
(K OW L AH N)
(K W EH S CH AH N M AA R K)
(B R EY S)
(L EH F T B R EY S)
(OW P EH N B R EY S)
(K L OW Z B R EY S)
(R AY T B R EY S)

Ah, because those first bunch of entries in the dictionary contain special characters, their spelling maps to nil. That’s fine, we can adjust our definition to simply omit the pairs starting with nil.

(def spellings+phonemes
  (->>
   dictionary-lines
   (map (fn [line]
          (->>
           (clojure.string/split line #"\s") ; split lines by space
           (filter #(not-empty %))           ; remove empty strings (from whitespace separation)
           (map normalize-string)            ; normalize
           (split-at 1)                      ; split into spelling + phonemes
           ((fn [[[spelling] phonemes]] [spelling phonemes]))))) ; destructure the spelling list
   (filter #((complement nil?) (first %)))))

#'user/spellings+phonemes

Homo[phone|graph]s

Something we haven’t contended with yet are homophones, that is, words which have the same pronunciation, but distinct spellings (e.g. red and read).

Dually, there is the problem of homographs, that is, words which have the same spelling, but distinct pronunciations (e.g. the “long-e” read and the “short-e” read).

Our dictionary has entries of each kind, let’s check them out

Homophones

Let’s look at homophones first. Finding these things is not actually a trivial thing with such a large data set. A naive solution might go through each entry and check the rest of the list to see if that spelling occurs again.

However, because spellings+phonemes is a list, this would mean n comparisons for each of the n entries, that’s O(n^2), and in this case n is a large number (all words in the English dictionary), so that’s not quite going to work out for us.

Luckily this is a classic algorithms problem, and probably, like, question 3 on hackerrank or leetcode. I’ll spoil it for you.

The answer is to use a map.

As we traverse the list of [spelling phonemes], we insert each spelling as the key of a map (ostensibly a constant-time operation), and use the [phonemes] as the value. If we find another spelling which is exactly the same, the key will match in our list, and we can append the newer phonemes to the value.

Clojure has an awesome standard library, and maps are bread-and-butter Clojure data structures, so I can avoid the whole “look up the key in the map, if it does not exist insert an array, otherwise append to that array” by using the standard function merge-with.

Here’s the clojuredoc for merge-with:

clojure.core/merge-with [f & maps] Added in 1.0 Returns a map that consists of the rest of the maps conj-ed onto the first. If a key occurs in more than one map, the mapping(s) from the latter (left-to-right) will be combined with the mapping in the result by calling (f val-in-result val-in-latter).

Ok, so how am I going to use this function to solve my problem? I am going to convert each [spelling phonemes] pair (which at this point more accurately represents a [spelling pronunciation] pair) into a map of {spelling [pronunciation]}, and then merge all of those maps using the into function to conjoin all the [pronunciations]

(into [1 2 3] [4 5 6])

[1 2 3 4 5 6]

Let’s try it:

(rand-nth (map (fn  [[spelling pronunciation]] {spelling [pronunciation]}) spellings+phonemes))

{"HUGGED" [("HH" "AH" "G" "D")]}

Cool, so now we have a list of maps with 1 key-value pair each, we have to reduce that to a single map with merge-with:

(def word->pronunciations
  (reduce
   (partial merge-with into)
   (map (fn  [[spelling pronunciation]] {spelling [pronunciation]}) spellings+phonemes)))

#'user/word->pronunciations

(.get word->pronunciations "ICE")
(.get word->pronunciations "CREAM")

[(“AY” “S”)]
[(“K” “R” “IY” “M”)]

Hooray! We can now find the pronunciation for any English word.

Exploring the pronunciations

Let’s see if we can get a word with multiple pronunciations:

(rand-nth (filter (fn [[k v]] (> (.length v) 1)) word->pronunciations))

["AYDAR" [("AY" "D" "AA" "R") ("EY" "D" "AA" "R")]]

Hmm, I’m curious which word has the most pronunciations?

(let [maxlen (apply max (map (fn [[k v]] (.length v)) word->pronunciations))]
  (filter (fn [[k v]] (.equals (.length v) maxlen)) word->pronunciations))

(["M" [("EH" "M") ("EH" "M" "W" "AH" "N") ("EH" "M" "T" "UW") ("EH" "M" "TH" "R" "IY") ("EH" "M" "F" "AO" "R") ("EH" "M" "F" "AY" "V")]] ["C" [("S" "IY") ("S" "IY" "W" "AH" "N") ("S" "IY" "T" "UW") ("S" "IY" "TH" "R" "IY") ("S" "IY" "F" "AO" "R") ("S" "IY" "F" "AY" "V")]])

Oh, I guess “M1”, “M2”, “M3”… and “C1”, “C2”, “C3” … are all valid words in the dictionary and I broke them by removing the numbers. Whatever.

How about the next-most pronunciations?

(let [maxlen (apply max (map (fn [[k v]] (.length v)) word->pronunciations))]
  (filter (fn [[k v]] (= (.length v) (- maxlen 1))) word->pronunciations))

(["CAT-" [("K" "AE" "T" "W" "AO" "N") ("K" "AE" "T" "T" "UW") ("K" "AE" "T" "TH" "R" "IY") ("K" "AE" "T" "F" "AO" "R") ("K" "AE" "T" "S" "IH" "K" "S")]])

Hurricanes, cool. Again, I removed the numeric value from the word itself, but that shouldn’t really matter.

I want to find the first real word though…

(let [maxlen (apply max (map (fn [[k v]] (.length v)) word->pronunciations))]
  (take 1 (filter (fn [[k v]] (= (.length v) (- maxlen 2))) word->pronunciations)))

(["GRANTED" [("G" "R" "AE" "N" "T" "AH" "D") ("G" "R" "AE" "N" "T" "IH" "D") ("G" "R" "AE" "N" "AH" "D") ("G" "R" "AE" "N" "IH" "D")]])

This is pretty interesting! The last two pronunciations completely omit the “T” sound from “GRANTED”, which is known linguistically as elision. We say that the “T” was elided from the pronunciation of “GRANTED”.

What makes a Map?

Why did I name our data structure word->pronunciations? The A->B naming convention is common in Lisp-like languages to describe functions which map one data type to another, but what we’ve created is supposed to be a map, not a function, right? Well, Clojure doesn’t make the distinction so severe, since the map data structure is basically a function that converts from the key type to the value type.

In most languages, (like JavaScript), if you want to get a value out of a map (object in JavaScript), you have to write code that looks like this:

my_map[key]

and to call a function you have to write code that looks like this:

my_function(key)

but in Clojure, if you have a map, you can call it like you would a function (since it is a function):

({:a 1} :a)

We are using this fact to our advantage in our definition of word->pronunciations.

;; A map is a data structure (object)...
(.get word->pronunciations "ICE")
;; ...but also a function!
(word->pronunciations "ICE")

[(“AY” “S”)]
[(“AY” “S”)]

Homographs

Now, homographs are a very similar problem, except in reverse. This time, we want words which have the same pronunciation to be associated.

Lucky for us, Clojure’s maps and lists are fantastic data structures, and compose beautifully.

(= '("AY" "S") '("AY" "S"))

true

This is awesome. If two lists contain the same strings, then they’re treated as equivalent!

JavaScript (arrays, since there are no “lists”) is not so friendly:

console.log(["AY","S"] === ["AY","S"]);
console.log(["AY","S"] == ["AY","S"]);

false
false
undefined

The implication here is that our lists will collide in our map, meaning to get a function mapping pronunciation->words, all we need to do is reverse the keys and values:

(def pronunciation->words
  (reduce
   (partial merge-with into)
   (map (fn  [[spelling pronunciation]] {pronunciation [spelling]}) spellings+phonemes)))

#'user/pronunciation->words

(pronunciation->words '("AY" "S"))

["ICE"]

`sentence->pronunciations`

Now that we can go from a word to a list of pronunciations (word->pronunciation), it shouldn’t be too hard to go from a list of words (AKA a sentence) to a list of pronunciations (sentence->pronunciations).

The only complication: what should we do if a word has multiple pronunciations? How should you pronounce that sentence?

Well, each time a word has multiple pronunciations, we should probably return a new pronunciation for the whole sentence. The word “READ” has 2 pronunciations:

(word->pronunciations "READ")

[("R" "EH" "D") ("R" "IY" "D")]

So the (nonsensical) sentence “READ READ” should produce 4 pronunciations:

("R" "EH" "D" "R" "EH" "D")
("R" "EH" "D" "R" "IY" "D")
("R" "IY" "D" "R" "EH" "D")
("R" "IY" "D" "R" "IY" "D")

This type of combination is a cartesian product, and Clojure has an implementation built into the clojure.math.combinatorics namespace. Unfortunately that namespace needs to be included as a leiningen dependency, and I haven’t figured out yet how to get that to work correctly with the literate programming environment I’m using (org-babel), so I’ll just include a cartesian-product function in this script

(defn cart [colls]
  "Cartesian product on the list of collections"
  (if (empty? colls)
    '(())
    (for [more (cart (rest colls))
          x (first colls)]
      (cons x more))))

#'user/cart

(cart [[]])
(cart [[] [2]])
(cart [[1] [2]])
(cart [[1 3] [2]])
(cart [[1 3] [2 4]])
(cart [[1 3] [2 4] [5 6]])

()
()
((1 2))
((1 2) (3 2))
((1 2) (3 2) (1 4) (3 4))
((1 2 5) (3 2 5) (1 4 5) (3 4 5) (1 2 6) (3 2 6) (1 4 6) (3 4 6))

Given this definition, the pronunciations of a sentence are merely the cartesian product of the pronunciations of all the words (normalized to capital letters and split by spaces, of course):

(defn sentence->words
  [sentence]
  (->
   sentence
   (clojure.string/upper-case)
   (clojure.string/split #"\s")))

#'user/sentence->words

(sentence->words "Luke I am your father.")

["LUKE" "I" "AM" "YOUR" "FATHER."]

(defn sentence->pronunciation
  [sentence]
  (cart (map word->pronunciations (sentence->words sentence))))

#'user/sentence->pronunciation

(sentence->pronunciation "READ READ")

((("R" "EH" "D") ("R" "EH" "D")) (("R" "IY" "D") ("R" "EH" "D")) (("R" "EH" "D") ("R" "IY" "D")) (("R" "IY" "D") ("R" "IY" "D")))

Actually, we should flatten each of those results as well, to get a list of strings instead:

(defn sentence->pronunciation
  [sentence]
  (map flatten (cart (map word->pronunciations (sentence->words sentence)))))

#'user/sentence->pronunciation

(sentence->pronunciation "READ READ")

R	EH	D	R	EH	D
R	IY	D	R	EH	D
R	EH	D	R	IY	D
R	IY	D	R	IY	D

(sentence->pronunciation "Please not while I'm eating")

P	L	IY	Z	N	AA	T	W	AY	L	AY	M	IY	T	IH	NG
P	L	IY	Z	N	AA	T	HH	W	AY	L	AY	M	IY	T	IH	NG
P	L	IY	Z	N	AA	T	W	AY	L	AH	M	IY	T	IH	NG
P	L	IY	Z	N	AA	T	HH	W	AY	L	AH	M	IY	T	IH	NG

`pronunciation->sentence`

Now that we can generate the pronunciation of a sentence, we will want to be able to go from a pronunciation to a sentence.

The way I imagine the mondegreen generator working is roughly:

sentence -> pronunciation -> sentence

where the first sentence and last sentence are different. Consider the classic:

I scream -> ice cream

As we can see, their pronunciations match exactly:

(sentence->pronunciation "I scream")
(sentence->pronunciation "ice cream")

((“AY” “S” “K” “R” “IY” “M”))
((“AY” “S” “K” “R” “IY” “M”))

So how can we go from that representation to either of the two sentences?

Trie

What we will need is a way to, given a phoneme, get a list of the possible phonemes which are part of a valid English word.

So, if given just "AY", this function should tell us that, indeed "AY" is part of the valid word I, but also that "S" is a valid continuation after "AY" (since "S" is the next phoneme in "ICE").

I think it was my freshman-year Fundamentals of Computer Programming professor Olin Shivers (but he might have been quoting someone) who said (and I’m probably poorly paraphrasing):

Your data structures must be smart so your algorithms can be dumb.

I thought this was a perlism (whom professor Shivers was fond of), but I couldn’t find it in the list.

Well, what we want here is a data structure which is smart enough to answer our question.

I immediately considered the trie.

It’s awesome, just a nested map, but powerful enough to be the core data structure powering Lucene (which in turn powers ElasticSearch). Tries are all about re(trie)val, they retrieve information based on partial data.

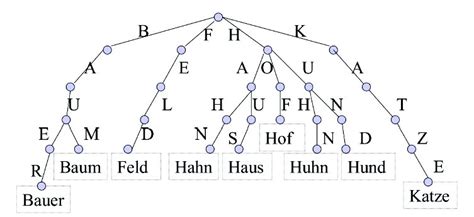(excuse the German, it was the best diagram I could find on DuckDuckGo)

Our trie will be a potentially 26-ary tree (one for each possible next letter), which we will choose to represent as nested maps, with nodes representing either letters or complete terms.

In our case though, the nodes won’t be letters, but phonemes! That way, we can traverse the trie, looking for the next phoneme in our sentence.

Let’s try constructing the trie. We can use the same map-merging trick we used to create word->phonemes.

I want to create the following map for the word “READ”:

{ "R" { "EH" { "D" "What to associate here?" }}}

This should embed the phoneme structure, but when we actually finish a word we have to indicate that, while not blocking any further phonemes.

I’ll choose to use the keyword :word:

{ "R" { "EH" { "D" { :word "RED" "IY" { :word "READY" ... more phonemes ... } } }}}

(defn word->nested-map
  [phones word]
  (if (empty? phones)
    { :word word }
    { :word nil
      (first phones) (word->nested-map (rest phones) word)}))

#'user/word->nested-map

(word->nested-map '("R" "EH" "D") "RED")

{:word , "R" {:word , "EH" {:word , "D" {:word "RED"}}}}

Now to merge.

Unfortunately Clojure’s merge-with function only works for a single level of map, but we will want to deep-merge them. Actually, we’ll have to deep-merge-with them, since some of the phoneme maps are bound to collide.

I’m not above using other people’s code, and the clojuredocs website has awesome comments with community suggestions. I pulled this implementation from the comments on the built-in merge-with:

(defn deep-merge-with
  "https://clojuredocs.org/clojure.core/merge-with#example-5b80843ae4b00ac801ed9e74
  Like merge-with, but merges maps recursively, applying the given fn
  only when there's a non-map at a particular level."
  [f & maps]
  (apply
   (fn m [& maps]
     (if (every? map? maps)
       (apply merge-with m maps)
       (apply f maps)))
   maps))

#'user/deep-merge-with

(deep-merge-with + {:a {:b {:c 1 :d {:x 1 :y 2}} :e 3} :f 4}
                   {:a {:b {:c 2 :d {:z 9} :z 3} :e 100}})

{:a {:b {:c 3, :d {:x 1, :y 2, :z 9}, :z 3}, :e 103}, :f 4}

Now, we will also need a way to handle our homophones, so :word will actually have to be an array, and the function we merge-with will have to be able to handle insert into that array.

(defn merge-with-nil
  [a b]
  (cond (nil? a) b
        (nil? b) a
        :else (into a b)))

#'user/merge-with-

(merge-with-nil nil nil)
(merge-with-nil [1] nil)
(merge-with-nil nil [1])
(merge-with-nil [1] [2])

[1]
[1]
[1 2]

So now creating our trie is simple:

(def pronunciations-trie
  (apply
   deep-merge-with
   merge-with-nil
   (map (fn [[pronunciation word]] (word->nested-map pronunciation word)) pronunciation->words)))

#'user/pronunciations-trie

To get at words in the trie, we need to recursively get phonemes, and finally select the word:

(->
 pronunciations-trie
 (.get "R")
 (.get "EH")
 (.get "D")
 (:word))

["READ" "READE" "RED" "REDD"]

We can use Clojure’s loop macro to define a function which will check if a list of phonemes is a valid pronunciation of some English word.

In our case we don’t just want to return true or false, but the actual trie structure that the pronunciation results in. This will let us continue to look up words based on where we leave off.

(defn lookup-pronunciation
  [pronunciation]
  (loop [remaining pronunciation
         trie pronunciations-trie]
    (cond (empty? remaining) trie
          (nil? trie) nil
          :else (recur (rest remaining) (trie (first remaining))))))

#'user/lookup-pronunciation

(:word (lookup-pronunciation ["R" "EH" "D"]))
(:word (lookup-pronunciation ["D" "EY"]))

[“READ” “READE” “RED” “REDD”]
[“DAE” “DAY” “DAYE” “DE” “DEY”]

Weird Results

Honestly, some of these results are weird. If I was playing this game and came across “DE” I would probably pronounce it as ["D" "EE"] not ["D" "EY"]. One way we can consider fixing this is by finding a list of the most common English words, and filter our original dictionary to only include those words. That ought to exclude the weirder words like "DE", "READE", "REDD" etc.

TODO Do that. I don’t have a list of the most common words yet.

Substitutions

A key aspect of the Mondegreens which I haven’t discussed yet are sound substitutions. For example, many Mondegreens will slightly change a syllable here or there to through the reader off slightly, but usually the sound will be sufficiently close so the reader can still guess correctly. The type of substitutions I see are usually phonetically similar, like "D"->"T" (both are known linguistically as frontal stops, where "D" is the alveolar stop and "T" is the dental stop. "D" is voiced (your throat hums when you pronounce it), and "T" is unvoiced).

Mathematically, when we want to express equivalence between objects, we can put them in the same Set.

I’ve created a list of Sets of phonemes which I consider to be valid substitutions for each other in our game, but these, while guided by my limited knowledge of phonetics, are more or less arbitrary.

Singleton classes represent phonemes which I don’t think should be replaced with anything else.

(def equivalence-classes
  "It would be better to base these substitutions on some kind of linguistic data. I bet it exists."
  [#{"AA" "AO" "AW" "AH" "UH"} ; all pretty similar vowel sounds
   #{"AY"}
   #{"B"}
   #{"CH"}
   #{"D"}
   #{"DH" "TH"} ; The difference in the "TH" sound between "these" and "teeth"
   #{"EH" "IH"}
   #{"EY"} ; Maybe can be paired up?
   #{"ER" "R"}
   #{"F"}
   #{"G" "K"} ; voiced vs. unvoiced glottal stops
   #{"HH" nil} ; The "H" sounds often gets deleted from mondegreens, so this indicates it is equivalent to no sound.
   #{"IY"} ; Maybe goes with "IH", but probably not "EH"... Maybe these shouldn't be sets?
   #{"JH" "ZH"} ; I forget the linguistic difference between these, but it's "EDGE" vs. "JACQUE"
   #{"L"}
   #{"M"}
   #{"N"}
   #{"NG"} ; Can go with N+G when splitting one phoneme into multiple is allowed.
   #{"OW"} ; All diphthongs can probably go with their constituent monophthongs. e.g. AA+UW
   #{"OY"}
   #{"P"}
   #{"SH"} ; Maybe belongs with "S"
   #{"T"} ; Can this go with "D"? Is that too jarring?
   #{"V"}
   #{"W"}
   #{"Y"}
   #{"S" "Z"}])

#'user/equivalence-classes

This is honestly a pretty conservative interpretation of which phonemes are close enough for our game, and if I were to really perfect this program, this is where I would focus.

Now that we have the classes, we can answer the question “Given a phoneme, what are its valid replacements for our game?”:

(defn valid-replacements
  [phoneme]
  (mapcat (partial apply vector) (filter #(% phoneme) equivalence-classes)))

#'user/valid-replacements

(valid-replacements "AY")
(valid-replacements "AA")
(valid-replacements "S")
(valid-replacements "Z")
(valid-replacements "HH")

(“AY”)
(“UH” “AH” “AW” “AA” “AO”)
(“S” “Z”)
(“S” “Z”)
( “HH”)

Finding a sentence given a pronunciation

Now to combine what we have done so far.

Let’s manually walk through an example sentence that we know works so that we can piece together our algorithm.

"I SCREAM"

First, we turn it into a pronunciation:

(sentence->pronunciation "I SCREAM")

(("AY" "S" "K" "R" "IY" "M"))

Cool, only 1 possible pronunciation to worry about.

Next, we need to recursively ask whether our phonemes make up a word:

(lookup-pronunciation ["AY"])
 ; no?
(lookup-pronunciation ["AY" "S"])
 ; no?
(lookup-pronunciation ["AY" "S" "K"])
...

Or whether any of the valid replacements for each of our phonemes make up a word:

(defn pronunciation->sentence
  [pronunciation]
  (letfn [(find-pronuns
            [prev-phones next-phones]
            (let [answer (:word (lookup-pronunciation prev-phones))]
              (cond (empty? next-phones) answer  ; whether or not it is valid, we have no more phonemes to work with
                    answer (cons answer (find-pronuns [] next-phones)) ; we found a real word, just worry about the next set of phonemes then
                    :else (reduce (fn [acc x] (or acc (find-pronuns (conj prev-phones x) (rest next-phones))))
                                  nil
                                  (valid-replacements (first next-phones))))))]
    (find-pronuns [] pronunciation)))

#'user/pronunciation->sentence

(pronunciation->sentence (first (sentence->pronunciation "I SCREAM")))

(["AI" "AY" "AYE" "EYE" "I" "I."] "SCREAM")

Ok, so we got our original sentence more or less. To prevent that, let’s pass in the a set of the words in the original sentence, and make sure we don’t return any of those. Technically this will exclude a set of potential solutions where a word in the original sentence occurs somewhere completely different in the Mondegreen sentence, e.g. if you had the sentence “I SCREAM ICE-CREAM”, a valid Mondegreen would technically be “ICE-CREAM I SCREAM”, but I’ll just ignore that set of solutions in favor of something which doesn’t contain any words from the original.

(defn pronunciation->sentence
  "Can this series of phonemes be parsed as a collection of English words? Find one answer containing no words from the set of words in the original sentence."
  [pronunciation original-sentence]
  (letfn [(word? [phones]
            (let [words (:word (lookup-pronunciation phones))]
              (and (not (some #(original-sentence %) words)) (first words))))
          (search-substitutions
            [prev-phones next-phones]
            (reduce (fn [acc x] (or acc (find-pronuns (conj prev-phones x) (rest next-phones))))
                    nil
                    (valid-replacements (first next-phones))))
          (find-pronuns [prev-phones next-phones]
            (let [answer (word? prev-phones)]
              (cond
                (empty? next-phones) (when answer (list answer))
                answer (if-let [rest-of-sentence (find-pronuns [] next-phones)]
                         (cons answer rest-of-sentence)
                         (search-substitutions prev-phones next-phones))
                :else (search-substitutions prev-phones next-phones))))]
    (find-pronuns [] pronunciation)))

#'user/pronunciation->sentence

We achieve this by taking the set of words from the original sentence and comparing the possible word for the phonemes so far against that set.

So in the "I SCREAM" example:

(pronunciation->sentence (first (sentence->pronunciation "I SCREAM")) (set (sentence->words "I SCREAM")))

("ICE" "CREAM")

So in this case, the algorithm found "I" as a possible word for the phoneme list '("AY"), but since that was part of our original sentence, it disregarded it and continued until it found "ICE".

(set (sentence->words "I SCREAM"))
(:word (lookup-pronunciation '("AY")))
(some #((set (sentence->words "I SCREAM")) %) (:word (lookup-pronunciation '("AY"))))

#{“SCREAM” “I”}
[“AI” “AY” “AYE” “EYE” “I” “I.”]
“I”

Mondegreen

Now that we have pronunciation->sentence, we basically have our entire mondegreen generator. All that’s left is to expose a convenient wrapper to do the parsing of inputs.

(defn mondegreen
  [sentence]
  (let [sentence-phonemes (sentence->pronunciation sentence)
        sentence-words (set (sentence->words sentence))]
    (pronunciation->sentence (first sentence-phonemes) sentence-words)))

#'user/mondegreen

(mondegreen "I SCREAM")
(mondegreen "ICE-CREAM")
(mondegreen "PLEASE NOT WHILE I'M EATING")
(mondegreen "SOMEONE STOLE MY LEMON TREE")

(“ICE” “CREAM”)
(“AI” “SCREAM”)
(“PLEA” “SNOUT” “WAI” “LAI” “ME” “TENG”)
(“SOME” “ONCE” “TOAL” “MILE” “EH” “MUN” “TER” “E”)

One of the implications of this particular algorithm is that it will prefer the shortest words first. This also decreases search time, but could lead to boring results over time. The same short words, like “EH”, “E”, “TER”, comprising only one or two phonemes will appear most often. You would be hard-pressed to find two- or three-syllable results ever appear. Maybe these will be improvements I will make, but I’m actually working on an implementation of the same exact program in SBCL Prolog, so I might never need to put in that work here ;)

Matthew DiLoreto